二分查找，一个看似简单却复杂的算法解析

发表于 更新于 分类于 阅读次数： Valine：

引言

二分查找的大名，如雷贯耳，它可以在有序的一个数组中实现实现$O(logn)$的复杂度查找。

然而，业界还流传着一句话

十个二分九个错

这句调侃的话可谓精准的描述了二分查找的特性，二分查找从实现思路上是非常简单的，利用有序特性，对半查找，不断缩小范围，直到找到结果。然而在细节边界问题上，二分查找可以说是难得过分，如：

  • 退出循环的标准，是< 还是 <= ?
  • mid的计算标准，是(left+right)/2还是 (left+right+1)/2 ?
  • 折半的移动标准，是 =mid 还是 =mid-1 ?
  • 返回值的选定，怎么有写是left，有写是right，有写还要额外判断？

因为这些边界问题，导致二分查找以为懂了的你，写出的代码总是不行，本文为个人为了彻底弄懂二分查找，一劳永逸的从根本上理解的沉淀。

二分查找的核心思想

二分查找的核心思想就是对半查找，如下图所示，有一个[1,2,3,4,5,6,7] 数组，要判断2是否存在于这个数据中。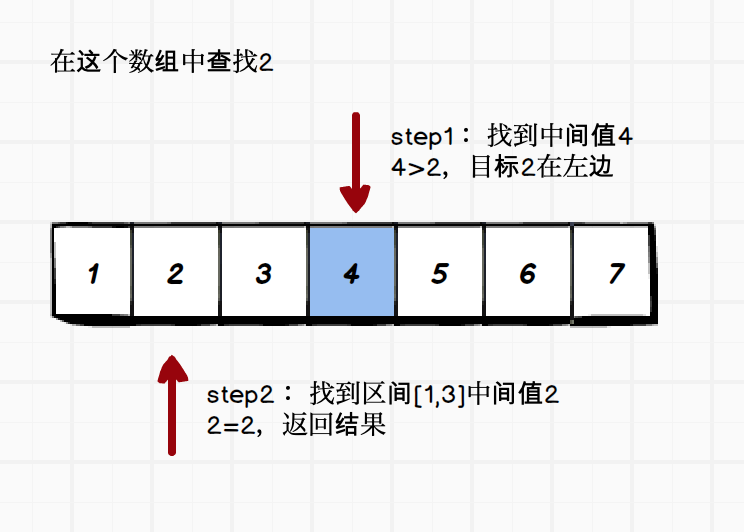

二分查找的方法为：

  1. 数组[1,2,3,4,5,6,7]的中间值为 (1+7)/2=4，找第四个数字，该值为4，由于4!=2，因此需要继续判断，又由于4>2，因此得出目标值在左边这个区间，即[1,2,3]这里面
  2. 数组[1,2,3]的中间值为 (1+3)/2=2，找第二个数字，该值为2，是期望要找的目标，返回ture。

核心思想非常简单，非常简介。

二分查找的分类


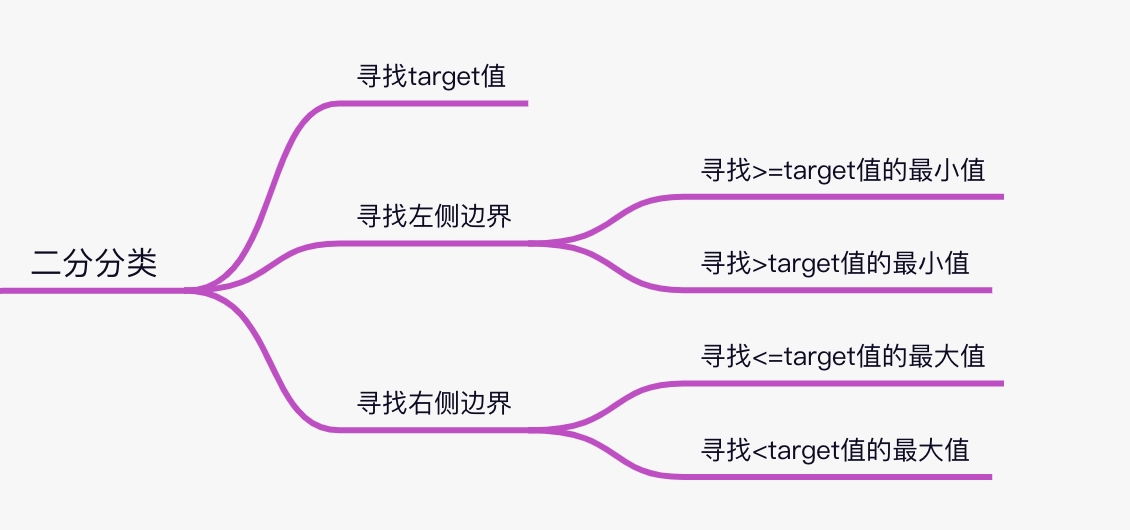
二分查找的类型可以分为

  • 寻找target值的下标
  • 寻找左侧边界
  • 寻找右侧边界
  • 寻找小于target值的最大值
  • 寻找>target值的最小值

其中
寻找左侧边界= 寻找>=target值的最小值
寻找右侧边界= 寻找<=target值的最大值

不同类型的二分代码

先直接给代码，之后再通过分析代码直接的异常点来确认为什么代码要这么写。

最简单的二分，寻找target值的下标

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
 /**
 * 最简单的二分，不会出错，判断目标值是否在array中
 * */
public int binarySearch(int[] array,int target){
    int l=0;
    int r=array.length-1;
    while (l<=r){
        int mid=(l+r)>>1;
        if(array[mid]==target){
            return mid;
        }else if(array[mid]<target){
            l=mid+1;
        }else{
            r=mid-1;
        }
    }
    return -1;
}

寻找左侧边界

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * 寻找左侧边界
 * */
public int binarySearchLeft(int[] array,int target){
    int l=0;
    int r=array.length-1;
    while (l<r){
        int mid=(l+r)>>1;
        if(array[mid]>=target){
            r=mid;
        }else{
            l=mid+1;
        }
    }
    return array[l]==target?l:-1;
}

寻找右侧边界

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * 寻找右侧边界
 * */
public int binarySearchRight(int[] array,int target){
    int l=0;
    int r=array.length-1;
    while (l<r){
        int mid=(l+r+1)>>1;
        if(array[mid]<=target){
            l=mid;
        }else{
            r=mid-1;
        }
    }
    return array[r]==target?r:-1;
}

寻找小于target的最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * 寻找小于target的最大值
 * */
public int binarySearchLtTarget(int[] array,int target){
    int l=0;
    int r=array.length-1;
    while (l<r){
        int mid=(l+r+1)>>1;
        if(array[mid]>=target){
            r=mid-1;
        }else{
            l=mid;
        }
    }
    return array[r]<target?r:-1;
}

寻找大于target的最小值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * 寻找大于target的最小值
 * */
public int binarySearchGtTarget(int[] array,int target){
    int l=0;
    int r=array.length-1;
    while (l<r){
        int mid=(l+r)>>1;
        if(array[mid]<=target){
            l=mid+1;
        }else{
            r=mid;
        }
    }
    return array[l]>target?l:-1;
}
  1. 区间判断采用闭区间

4步掌握二分查找写法

要想写出不出错的二分查找，必须得有区间思维，带着去见思维去写代码。个人总结了4步操作

1.二分查找框架模板伪代码

掌握二分查找框架模板，之后再一步一步实现细节，一个通用的模板如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 *  二分查找通用伪代码
 * */
public int binarySearch(int[] array,int target){
    int l=0;
    int r=array.length-1;
    while (loopCondition(l,r)){
        int mid=calcMid(l,r);
        if(check(array[mid],target)){
            l=changeLeft(mid);
        }else{
            r=changeRight(mid);
        }
    }
    return rs;
}

其中，exitLoopCondition,calcMid,check,changeLeft,changeRight,rs等都为伪代码，需要后续去实现。

2. 确认进入循环条件

确认进入循环的条件，即确认上文伪代码中的exitLoopCondition片段。

确认循环进入条件，首先确认我们的左右查询区间。

  • 如果是$[l,r]$的闭区间，那么判断条件应该为 l<=r
  • 如果是$[l,r)$的左闭又开区间，那么判断条件应该为 l<r

至于$(l,r]$左开右闭及$(l,r)$左开右开，由于太过特例独行，本篇就不进行考虑，当人个人可以进行推导。

所以，为什么$[l,r]$的闭区间，判断条件应该为$l<=r？$，而$[l,r)$的左闭又开区间，判断条件应该为 l<r？

对于二分查找，如果区间内不为空且存在值，那么就应该进入循环继续判断。
那么进入循环的条件判断就转化为，l，r满足什么条件，区间内存在值且不为空？
这个问题只要动用简单的数学知识，就能知道。

  • 对于闭区间$[l,r]$，当边界区间内有值的条件为$l<=r$，因此当$l<=r$时，都应该进入循环。
  • 而对于左闭右开区间$[l,r)$,边界的有值条件为$l<r$

是不是感觉和之前的话一模一样，但是视角不一样了。

3. mid值的计算

mid值的计算写法有很多种，本文列举几种

1
2
3
4
5
6
7
8
9
10
# 左边界
int mid=(l+r)/2;
int mid=(l+r)>>1;
int mid=l+(r-l)/2;
int mid=l+((r-l)>>1);
# 右边界
int mid=(l+r+1)/2;
int mid=(l+r+1)>>1;
int mid=l+(r-l+1)/2;
int mid=l+((r-l+1)>>1);

tips

  1. mid值可能溢出，因此如果可以，将int升级为long类型
  2. 位运算符比除号性能更好
  3. 求右边界时，需要+1
  4. 使用位运算符，注意位运算的计算优先级

4. 区间结果判断&区间变更

本段主要确认的代码为

1
2
3
4
5
if(check(array[mid],target)){
    l=changeLeft(mid);
}else{
    r=changeRight(mid);
}

从代码上来说，则是确认 l=mid,r=mid-1还是l=mid-1,r=mid

还是区间的概念，只要简单分析就明白了。

对于左开右闭区间$[l,r)$，二分后的区间应该为$[l,mid)$和$[mid,r)$

4.1 确认mid的归属，归属左半边还是右半边

常见问题

边界分类

文章参考